Official description

You will have to analyze the consumption traces of an early implementation of the AES made by Myster Mask. Will you be able to exploit these traces to make the difference?

The part to target corresponds to the inversion step in the calculation of the S-box in the first round of the AES. Only this step is implemented, it is not necessary to know the AES since this challenge is specifically focused on the inversion step.

The consumption traces provided correspond to the following call:

1

masked_inversion(L)

Beware! Myster Mask has protected this inversion by honoring his name. Now it’s your turn to play!

SHA256(traces.npz) = d4e16ded8c53f6e295672567cd8bdd3453ebd1318bf353b827c40cda17698fe4 SHA256(inputs.npz) = 283b4245a36d7d238ba941a247eaaa38cc90d8db2f3c4e7db824d241a6c21603

We get 4 files: traces.npz (side-channel traces), inputs.npz (plaintexts), myster_mask.py (the algorithm) and output.txt (the ciphertext to decode).

Myster Mask speaking

Exploration

output.txt contains an initial vector iv and a ciphertext c.

myster_mask.py shows how the masked algorithm works. We take a look at mask and unmask functions. After a bit of paper reading, we learn that this is a multiplicative 5 shares masking in Galois field 256 GF256.

Structure of the algorithm

The challenge description indicates that side-channel traces correspond to the execution of this function:

1
2
3
4
5
6

def masked_inversion(S):
    output = S
    for i in range(5):
        for j in range(16):
            output[j][i] = GF256(S[j][i]) ** 254
    return output

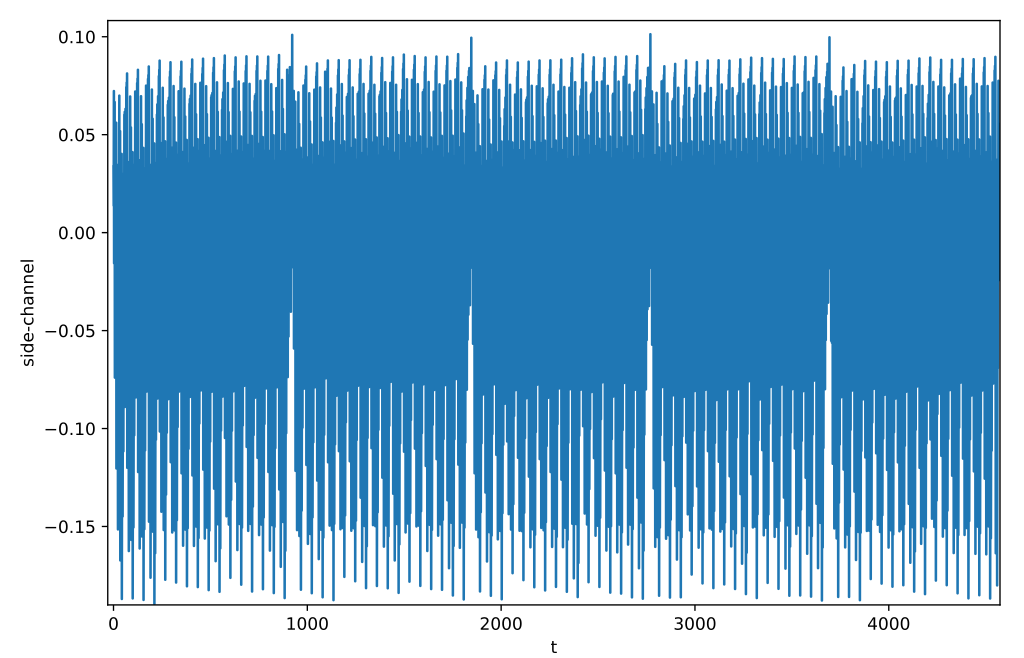
Average of traces.npy

We recognize in the averaging of all side-channel traces the 16 iterations of j in 5 iterations of i.

During the challenge I tried multiplying every 5 spikes corresponding to each masking share, then correlating each {key hypothesis XOR input} on them. I was unable to recover the key using this method.

Proposed solution

Multiplicative Masking and Power Analysis of AES, by Golić, J.D., Tymen, C. (2003) is a nice ressource to understand and solve this challenge. They introduce GF256 multiplicative masking then in section 2 explains how to setup a differential power analysis of AES.

As GF256(0) equals 0, calling mask(0) will always put a 0 in the first share. This implies that if key[i] and input[i] are equals, then key[i] XOR input[i] is 0 i.e. the masked first share is 0.

Let’s attack each \(i\)-th key byte separately. For each \(K\) key byte hypothesis, let’s filter \(M\) traces in which key[i] and input[i] are equals. Then we compare the average of \(M\) to the average trace. If the difference is the most important, then it means that the hypothesis may be the right key.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
from Crypto.Cipher import AES

inputs = np.load("inputs.npz")["inputs"]
traces = np.load("traces.npz")["traces"]

C = np.average(traces, axis=0)

key = [0] * 16
for i in range(16):
    max_diff = []
    for K in range(256):
        M = [trace for inp, trace in zip(inputs, traces) if inp[i]^K == 0]
        C_K = np.average(M, axis=0)
        max_diff.append(max(np.abs(C_K - C)))
    
    print(max(max_diff), np.argmax(max_diff))
    key[i] = int(np.argmax(max_diff))

# iv and c from output.txt
iv = bytes.fromhex("ec35aba34b09ddaf40133465cf99e0e4")
c = bytes.fromhex("592eefe2c8c2aa5cc4088909e80ed4342198<snip>")
d = AES.new(bytes(key), AES.MODE_CBC, iv=iv).decrypt(c)
print(d)

After some seconds, we get the flag:

0.03693260569852941 224
[...]
0.035091276041666675 63
b'FCSC{8e29ba7aa273cc1b3ea74defe5972fd7ff4a0180acf790bddb25980289c8
1d60}\n\t\t\t\t\t\t\t\t\t'